Optimize pgvector search

This guide explores how to effectively use pgvector for vector similarity searches in your AI applications. We'll address the following key questions:

1. How to profile your vector search queries, when using pgvector?
2. When to use indexes and tradeoffs between the available options?
3. Which parameters to tune for best performance?

We'll examine sequential scans, HNSW indexing, and IVFFlat indexing, providing benchmarks and practical recommendations for various dataset sizes. This will help you optimize pgvector queries in your Neon database for both accuracy and speed.

Without indexes, pgvector performs a sequential scan on the database and calculates the distance between the query vector and all vectors in the table. This approach does an exact search and guarantees 100% recall, but it can be costly with large datasets.

The query below uses EXPLAIN ANALYZE to generate an execution plan and display the performance of the similarity search query.

EXPLAIN ANALYZE SELECT * FROM items ORDER BY embedding <-> '[0.011699999682605267,..., 0.008700000122189522]' LIMIT 100;

This is what the query plan looks like:

Limit  (cost=748.19..748.44 rows=100 width=173) (actual time=39.475..39.487 rows=100 loops=1)
  ->  Sort  (cost=748.19..773.19 rows=10000 width=173) (actual time=39.473..39.480 rows=100 loops=1)
        Sort Key: ((vec <-> '[0.0117,..., 0.0866]'::vector))
        Sort Method: top-N heapsort  Memory: 70kB
        ->  Seq Scan on items  (cost=0.00..366.00 rows=10000 width=173) (actual time=0.087..37.571 rows=10000 loops=1)
Planning Time: 0.213 ms
Execution Time: 39.527 ms

You can see in the plan that the query performs a sequential scan (Seq Scan) on the items table, which means that the query compares the query vector against all vectors in the items table. In other words, the query does not use an index.

To understand how queries perform at scale, we tested sequential scan vector searches with pgvector on subsets of the GIST-960 dataset with 10k, 50k, 100k, 500k, and 1M rows using a Neon database instance with 4 vCPUs and 16 GB of RAM.

The sequential scan search performed reasonably well for tables with 10k rows (~36ms). However, sequential scans start to become costly at 50k rows.

So, when should you use sequential scans rather than defining an index?

• When your dataset is small and you do not intend to scale it.
• When you need 100% recall (accuracy). Adding indexes trades recall for performance.
• When you do not expect a high volume of queries per second, which would require indexes for performance.

Otherwise, consider adding an index for better performance.

Indexing with HNSW

HNSW is a graph-based approach to indexing multi-dimensional data. It constructs a multi-layered graph, where each layer is a subset of the previous one. During a vector similarity search, the algorithm navigates through the graph from the top layer to the bottom to quickly find the nearest neighbor. An HNSW graph is known for its superior performance in terms of speed and accuracy.

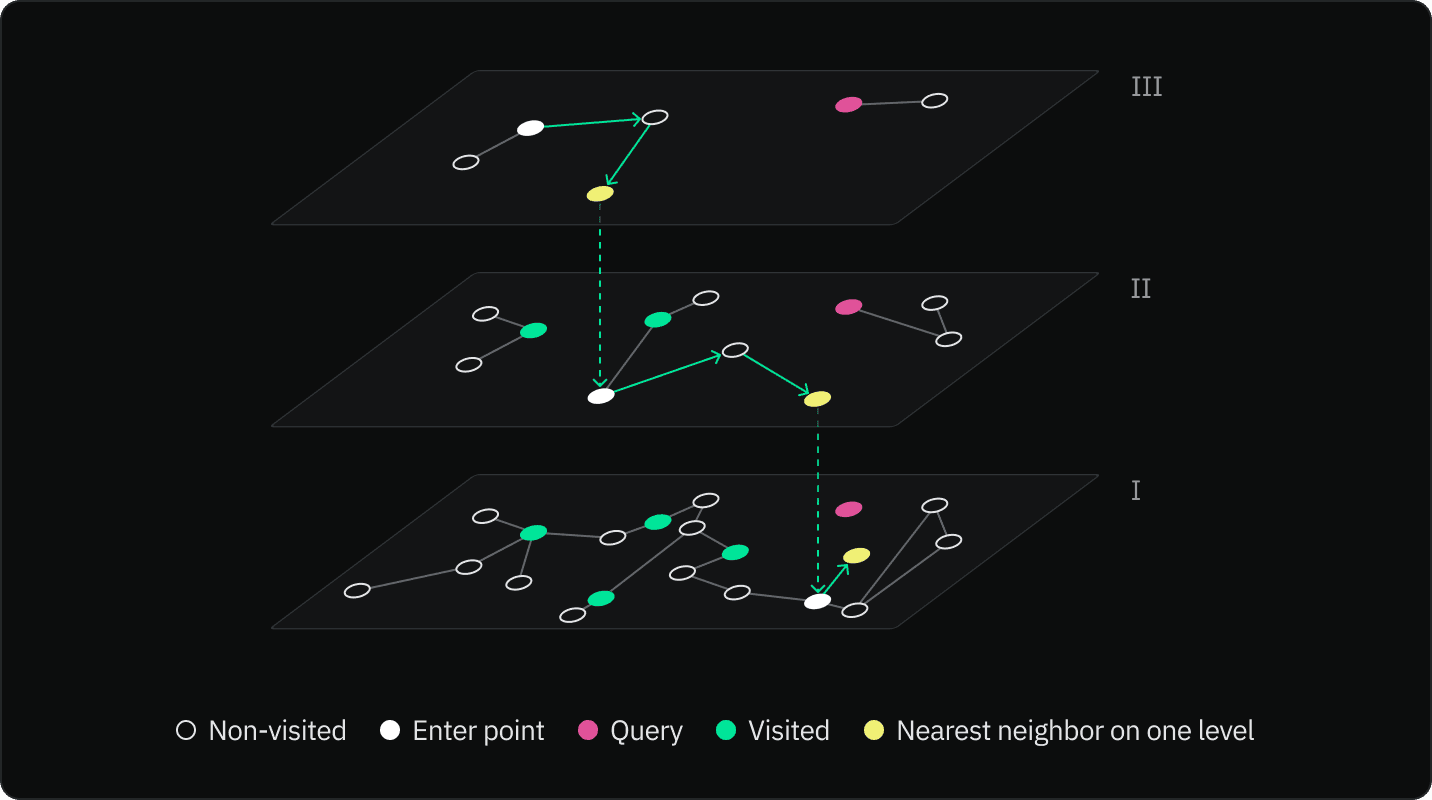
The search process begins at the topmost layer of the HNSW graph. From the starting node, the algorithm navigates to the nearest neighbor in the same layer. The algorithm repeats this step until it can no longer find neighbors more similar to the query vector.

Using the found node as an entry point, the algorithm moves down to the next layer in the graph and repeats the process of navigating to the nearest neighbor. The process of navigating to the nearest neighbor and moving down a layer is repeated until the algorithm reaches the bottom layer.

In the bottom layer, the algorithm continues navigating to the nearest neighbor until it cannot find any nodes that are more similar to the query vector. The current node is then returned as the most similar node to the query vector.

The key idea behind HNSW is that by starting the search at the top layer and moving down through each layer, the algorithm can quickly navigate to the area of the graph that contains the node that is most similar to the query vector. This makes the search process much faster than if it had to search through every node in the graph.

Tuning the HNSW algorithm

The following options allow you to tune the HNSW algorithm when creating an index:

• m: Defines the maximum number of links created for each node during graph construction. A higher value increases accuracy (recall), but it also increases the size of the index in memory and index construction time. Higher values are typically used with high-dimensionality datasets or when a high degree of accuracy is required. The default value is 16. Acceptable values for m typically fall between 2 and 100. For many applications, beginning with a range of 12 to 48 is advisable.
• ef_construction: Defines the size of the list for the nearest neighbors. This value influences the tradeoff between index quality and construction speed. A high ef_construction value creates a higher quality graph, enabling more accurate search results but also means that index construction takes longer. The value should be set to at least twice the value of m. The default setting is 64. There comes a point where increasing ef_construction no longer improves index quality. To evaluate search accuracy, you can start by setting ef_construction equal to ef_search and incrementally increasing ef_construction to achieve the desired result. If accuracy is lower than 0.9, there may be opportunity for improvement by increasing ef_construction.

This example demonstrates how to set the parameters:

CREATE INDEX ON items USING hnsw (embedding vector_l2_ops) WITH (m = 16, ef_construction = 64);

HNSW search tuning:

• ef_search: Defines the size of the dynamic candidate list for search. The default value is 40. This value influences the trade-off between query accuracy (recall) and speed. A higher value increases accuracy at the cost of speed. The value should be equal to or larger than k, which is the number of nearest neighbors you want your search to return (defined by the LIMIT clause in your SELECT query).

To configure this value, do so using a SET statement before executing queries:

SET hnsw.ef_search = 100;

You can also use SET LOCAL inside a transaction to set it for a single query:

BEGIN;
SET LOCAL hnsw.ef_search = 100;
SELECT ...
COMMIT;

In summary:

• To prioritize search speed over accuracy, use lower values for m and ef_search.
• Conversely, to prioritize accuracy over search speed, use a higher value for m and ef_search.
• Using a higher value for ef_construction yields more accurate search results at the cost of index build time.

Indexing with IVFFlat

IVFFlat indexes partition the dataset into clusters ("lists") to optimize for vector search.

You can create an IVFFlat index using the query below:

CREATE INDEX items_embedding_cosine_idx ON items USING ivfflat (embedding vector_l2_ops) WITH (lists = 1000);

IVFFlat in pgvector has two parameters:

1. lists

   • This parameter specifies the number of k-means clusters (or "lists") to divide the dataset into
   • Each cluster contains a subset of the data, and each data point belongs to the closest cluster centroid.

2. probes

   • This parameter determines the number of lists to explore during the search for the nearest neighbors.
   • By probing multiple lists, the search algorithm can find the closest points more accurately, balancing between speed and accuracy.

By default, the probes parameter is set to 1. This means that during a search, only one cluster is explored. This approach is fine if your query vector is close to the centroid. However, if the query vector is located near the edge of the cluster, closer neighbors in adjacent clusters will not be included in the search, which can result in a lower recall.

You must specify the number of probes in the same connection as the search query:

SET ivfflat.probes = 100;
SET enable_seqscan=off;
SELECT * FROM items ORDER BY embedding <-> '[0.011699999682605267,..., 0.008700000122189522]' LIMIT 100;

The output of this query appears as follows:

Limit  (cost=1971.50..1982.39 rows=100 width=173) (actual time=4.500..5.738 rows=100 loops=1)
  ->  Index Scan using items_embedding_idx on vectors  (cost=1971.50..3060.50 rows=10000 width=173) (actual time=4.499..5.726 rows=100 loops=1)
        Order By: (vec <-> '[0.0117, ... ,0.0866]'::vector)
Planning Time: 0.295 ms
Execution Time: 5.867 ms

We've experimented with lists equal to 1000, 2000, and 4000, and probes equal to 1, 2, 10, 50, 100, 200.

Although there is a substantial gain in recall for increasing the number of probes, you will reach a point of diminishing returns when recall plateaus and execution time increases.

Therefore, we encourage experimenting with different values for probes and lists to achieve optimal search performance for your queries. Good places to start are:

• Using a lists size equal to rows / 1000 for tables with up to 1 million rows, and sqrt(rows) for larger datasets.
• Start with a probes value equal to lists / 10 for tables up to 1 million rows, and sqrt(lists) for larger datasets.

Conclusion

The sequential scan approach of pgvector performs well for small datasets but can be costly for larger ones. Use sequential scans if you require 100% accuracy, but expect performance issues with higher volumes of queries per second.

You can optimize searches using HNSW or IVFFlat indexes for approximate nearest neighbor (ANN) search, but HNSW indexes have better query performance than IVFFlat with build time and memory usage tradeoffs.

Be sure to test different index tuning parameter settings to find the right balance between speed and accuracy for your specific use case and dataset.